Demystifying Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions

Related Articles: Demystifying Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Demystifying Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions

In the realm of digital logic design, Boolean expressions play a pivotal role in representing and manipulating complex circuits. However, the complexity of these expressions often poses a challenge, making it difficult to understand and implement efficient circuits. This is where Karnaugh maps (K-maps) emerge as a powerful tool, providing a visual and systematic approach to simplifying Boolean expressions and optimizing circuit designs.

Understanding Karnaugh Maps: A Visual Approach to Boolean Simplification

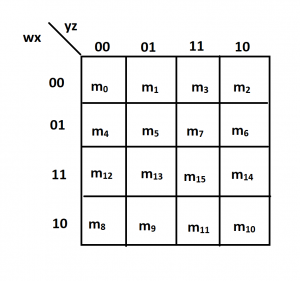
A Karnaugh map is a graphical representation of a truth table, designed to facilitate the identification and grouping of adjacent minterms (product terms) that share common variables. Each cell in the K-map corresponds to a unique combination of input variables, while the value within the cell represents the output of the function for that particular input combination.

The key to using K-maps lies in their unique arrangement. Unlike traditional truth tables, K-maps are structured in a way that ensures adjacent cells differ in only one variable. This arrangement allows for the identification of groups of adjacent cells with identical output values, representing a simplification opportunity.

The Power of Adjacency: Simplifying Boolean Expressions

The core principle behind K-map simplification lies in the concept of "adjacency." When two adjacent cells in a K-map contain the same output value, they can be grouped together, effectively eliminating a variable from the corresponding product term. This process of grouping adjacent cells, known as "looping," forms the basis for simplifying Boolean expressions.

The size and shape of the loops are crucial. A loop can encompass any number of adjacent cells, as long as they form a rectangular or square shape. The larger the loop, the more variables can be eliminated, leading to a more simplified expression.

Types of Karnaugh Maps: Tailoring the Tool for Different Scenarios

Karnaugh maps are available in various sizes and configurations, depending on the number of input variables in the Boolean expression. The most common types include:

• 2-Variable K-map: Used for functions with two input variables, it consists of a 2×2 grid.
• 3-Variable K-map: Used for functions with three input variables, it consists of a 2×4 grid.
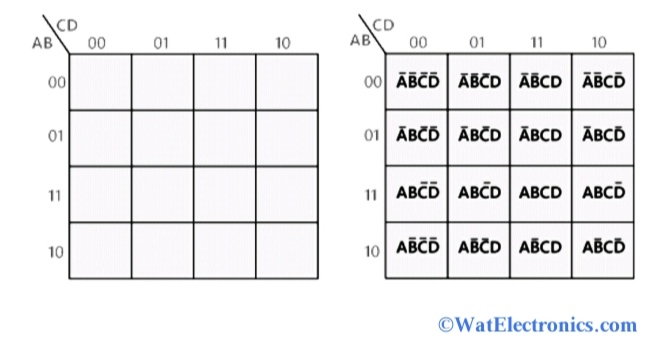
• 4-Variable K-map: Used for functions with four input variables, it consists of a 4×4 grid.

For higher numbers of variables, K-maps become increasingly complex and less practical. Alternative techniques, such as the Quine-McCluskey method, are more suitable for handling such scenarios.

Step-by-Step Guide to Using Karnaugh Maps: A Practical Approach

Simplifying Boolean expressions using K-maps involves a series of steps:

1. Construct the K-map: Determine the number of input variables and create a K-map of the appropriate size. Label the rows and columns with the input variables and their respective values.
2. Populate the K-map: Fill each cell in the K-map with the output value of the function for the corresponding input combination.
3. Identify adjacent groups: Look for groups of adjacent cells with the same output value. Remember that cells at the edges and corners of the map are considered adjacent.
4. Form loops: Encircle each group of adjacent cells with a loop. The loop should be as large as possible, forming a rectangle or square.
5. Write the simplified expression: For each loop, identify the variables that are common to all cells within the loop. The product term for the loop is formed by ANDing these common variables.
6. Combine the terms: The simplified expression is obtained by ORing the product terms corresponding to each loop.

Applications of Karnaugh Maps: Beyond Simplification

While simplification is the primary function of K-maps, their applications extend beyond this core purpose. They are widely used in:

• Circuit design: K-maps help in minimizing the number of logic gates required to implement a Boolean function, resulting in more efficient and cost-effective circuits.
• Logic optimization: K-maps can be used to identify redundant logic gates and simplify complex logic expressions, leading to improved circuit performance.
• Fault detection: By analyzing the K-map, engineers can identify potential faults in a circuit and develop strategies for fault detection and correction.

FAQs: Addressing Common Queries about Karnaugh Maps

Q1: What are the limitations of Karnaugh maps?

While powerful, K-maps have certain limitations:

• Limited to a few variables: For functions with more than five input variables, the complexity of K-maps becomes overwhelming.
• Handling don’t care conditions: Don’t care conditions, where the output value is irrelevant for specific input combinations, can be challenging to handle with K-maps.
• Manual process: The simplification process using K-maps is primarily manual, requiring careful attention to detail and understanding of the map’s structure.

Q2: What are the advantages of using Karnaugh maps?

K-maps offer several advantages:

• Visual representation: The graphical nature of K-maps provides a clear and intuitive way to understand and manipulate Boolean expressions.
• Systematic simplification: The process of looping and grouping adjacent cells provides a systematic and efficient method for simplifying expressions.
• Easy to understand: Compared to other simplification techniques, K-maps are relatively straightforward to learn and apply.

Q3: How can I improve my K-map skills?

Practicing is key to mastering K-maps. Here are some tips:

• Start with simple examples: Begin with basic Boolean expressions and gradually increase the complexity.
• Focus on understanding adjacency: Pay close attention to the concept of adjacency and how it applies to different K-map configurations.
• Use online tools: Numerous online tools and simulators can help you visualize and practice K-map simplification.

Conclusion: Embracing the Power of Visual Logic Simplification

Karnaugh maps provide a powerful and intuitive approach to simplifying Boolean expressions, enabling efficient circuit design and optimization. By understanding the fundamentals of K-maps, engineers can effectively minimize logic gates, improve circuit performance, and optimize their designs for cost-effectiveness and reliability. As a visual and systematic tool, K-maps remain an invaluable resource for logic designers, ensuring that complex Boolean expressions can be effectively simplified and translated into practical and efficient circuit implementations.

Closure

Thus, we hope this article has provided valuable insights into Demystifying Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions. We thank you for taking the time to read this article. See you in our next article!