Demystifying Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions

Related Articles: Demystifying Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Demystifying Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions

The realm of digital electronics thrives on the manipulation of binary logic, represented through Boolean expressions. These expressions, often complex and cumbersome, govern the behavior of digital circuits. Simplifying these expressions is crucial for achieving efficient and cost-effective designs. Enter the Karnaugh map (K-map), a powerful tool that transforms the tedious process of Boolean simplification into a visually intuitive and systematic one.

Understanding the Essence of Karnaugh Maps

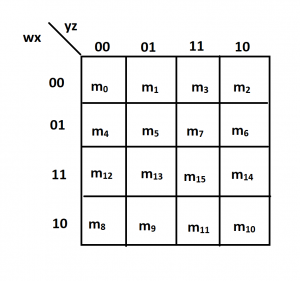
A Karnaugh map, named after its inventor Maurice Karnaugh, is a graphical representation of a truth table. It provides a visual framework for simplifying Boolean expressions by identifying and grouping together adjacent minterms (product terms) that represent the same output value. The map’s layout strategically arranges the minterms in a way that highlights these adjacencies, enabling a straightforward identification of redundant terms and subsequent simplification.

Constructing a Karnaugh Map: A Step-by-Step Approach

1. Identify the Number of Variables: The first step involves determining the number of input variables (n) in the Boolean expression. This determines the size of the K-map, requiring 2^n cells.

2. Define the Map’s Structure: The K-map is a grid-like structure where each cell represents a unique combination of input variables. The rows and columns are labeled with binary values representing the input variables. The arrangement ensures that adjacent cells differ in only one input variable.

3. Populate the Map with Output Values: Each cell in the K-map corresponds to a specific minterm. The output value of the expression for that minterm is entered into the corresponding cell.

4. Group Adjacency: The key to simplifying Boolean expressions lies in grouping together adjacent cells containing "1" values. These groups should be as large as possible and must be rectangular or square, with each group representing a simplified product term.

5. Derive the Simplified Expression: Each group of adjacent cells corresponds to a simplified product term. The variables that remain constant within the group form the product term. For example, a group where the variable ‘A’ is always ‘1’ and ‘B’ is always ‘0’ would result in the product term ‘A’ ‘B’ (or simply ‘A’ not ‘B’).

Illustrative Example: Simplifying a Boolean Expression Using a K-map

Consider the following Boolean expression:

F(A, B, C) = Σ(0, 1, 2, 4, 5, 6)

This expression represents a function with three input variables (A, B, C) and six minterms (0, 1, 2, 4, 5, 6). To simplify this expression using a K-map:

1. Construct the K-map: A 3-variable K-map requires 2^3 = 8 cells. The rows are labeled with the values of ‘C’ and ‘B’, and the columns with the values of ‘A’.

2. Populate the map: Enter "1" in the cells corresponding to the minterms (0, 1, 2, 4, 5, 6) and "0" in the remaining cells.

3. Group the cells: Identify the largest possible groups of adjacent cells containing "1" values. In this case, there are three groups:

   • Group 1: Covers minterms 0, 1, 4, and 5, resulting in the product term ‘A’ * ‘B’ (as ‘B’ is always ‘1’ and ‘A’ is always ‘1’ within this group).
   • Group 2: Covers minterms 2 and 6, resulting in the product term ‘C’ * ‘B’ (as ‘B’ is always ‘1’ and ‘C’ is always ‘1’ within this group).
   • Group 3: Covers minterm 0, resulting in the product term ‘not A’ ‘not B’ ‘not C’ (as all three variables are ‘0’ within this group).

4. Derive the simplified expression: The simplified expression is obtained by summing the product terms corresponding to each group:

   F(A, B, C) = ‘A’ ‘B’ + ‘C’ ‘B’ + ‘not A’ ‘not B’ ‘not C’

This simplified expression is equivalent to the original expression but is significantly more concise and efficient.

Advantages of Karnaugh Maps in Digital Circuit Design

1. Visual Simplification: K-maps provide a visual representation of the Boolean expression, making it easier to identify and group adjacent minterms for simplification. This intuitive approach eliminates the need for complex algebraic manipulations.

2. Efficiency: K-maps streamline the simplification process, reducing the time and effort required to arrive at the optimal expression.

3. Error Reduction: The visual nature of K-maps minimizes the risk of errors that can occur during manual algebraic simplification.

4. Enhanced Design: Simplified Boolean expressions lead to more efficient and cost-effective digital circuits, reducing the number of gates required and minimizing power consumption.

FAQs about Karnaugh Maps in Digital Electronics

1. What is the maximum number of variables that can be represented by a K-map?

The maximum number of variables that can be represented by a K-map is limited by the size and complexity of the map. However, it is generally practical to use K-maps for up to 5 or 6 variables. Beyond that, the map becomes too large and cumbersome to manage effectively.

2. Can K-maps be used to simplify expressions with "don’t care" conditions?

Yes, K-maps can handle "don’t care" conditions. These conditions represent input combinations where the output value is irrelevant. In the K-map, "don’t care" conditions are represented by ‘X’ and can be included in any group to further simplify the expression.

3. How do you handle K-maps with an odd number of input variables?

K-maps are typically designed for an even number of variables. To handle an odd number of variables, you can either:

* Use a larger K-map with the next higher even number of variables, leaving some cells unused.
* Treat the odd variable as a separate term and simplify the expression using a K-map for the remaining even variables.

4. What are some common mistakes to avoid while using K-maps?

• Incorrectly grouping cells: Ensure that groups are rectangular or square and include only adjacent cells.
• Missing essential prime implicants: These are prime implicants (simplified product terms) that are necessary for the complete representation of the function and cannot be omitted.
• Overlooking "don’t care" conditions: Utilize "don’t care" conditions to maximize group sizes and achieve further simplification.

Tips for Effective Karnaugh Map Utilization

• Start with a clear understanding of the Boolean expression: Carefully analyze the expression and identify the number of input variables and minterms.
• Use a systematic approach: Follow the steps for constructing and populating the K-map diligently.
• Prioritize larger groups: Aim to create the largest possible groups of adjacent cells to maximize simplification.
• Consider "don’t care" conditions: Include "don’t care" conditions in your groups whenever possible to further simplify the expression.
• Verify the simplified expression: After deriving the simplified expression, verify its correctness by comparing it to the original expression or by evaluating its truth table.

Conclusion: The Power of Karnaugh Maps in Digital Electronics

Karnaugh maps provide a valuable tool for simplifying Boolean expressions, enhancing the efficiency and effectiveness of digital circuit design. By leveraging the visual representation and systematic grouping of minterms, K-maps streamline the simplification process, reducing complexity and minimizing the number of gates required. This results in more cost-effective, power-efficient, and reliable digital circuits, demonstrating the enduring importance of this technique in the field of digital electronics.

Closure

Thus, we hope this article has provided valuable insights into Demystifying Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions. We appreciate your attention to our article. See you in our next article!