Demystifying the Karnaugh Map: A Comprehensive Guide to Four-Variable Simplification

Related Articles: Demystifying the Karnaugh Map: A Comprehensive Guide to Four-Variable Simplification

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Demystifying the Karnaugh Map: A Comprehensive Guide to Four-Variable Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying the Karnaugh Map: A Comprehensive Guide to Four-Variable Simplification

The realm of digital logic design is often characterized by complex Boolean expressions that govern the behavior of circuits. Simplifying these expressions is crucial for designing efficient and cost-effective circuits. One powerful tool that aids in this simplification process is the Karnaugh map (K-map). This article delves into the intricacies of K-maps, focusing specifically on their application to four-variable Boolean expressions.

Understanding the Essence of Karnaugh Maps

The Karnaugh map, named after its inventor Maurice Karnaugh, provides a visual representation of Boolean expressions. It leverages the concept of adjacency to identify and group together adjacent minterms (product terms), thereby simplifying the original expression. Each cell in the map corresponds to a unique combination of input variables, and the arrangement of cells ensures that adjacent cells differ in only one variable.

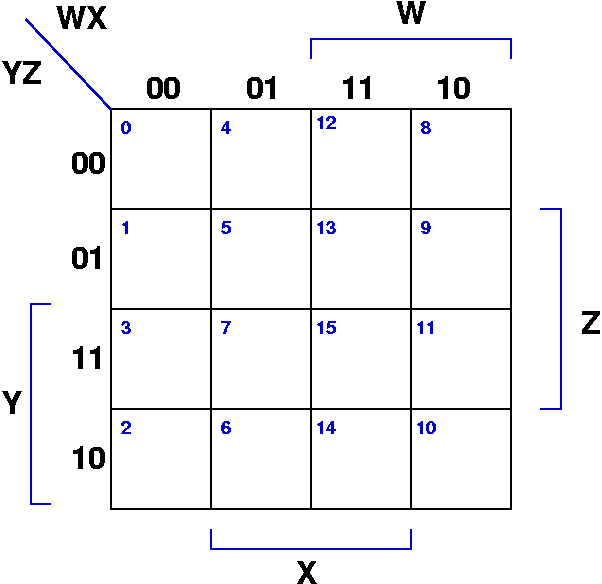
Constructing a Four-Variable Karnaugh Map

A four-variable K-map consists of a 2×4 grid, with each row and column representing a combination of two variables. The rows and columns are labeled in Gray code, a binary code where only one bit changes between adjacent values. This arrangement is crucial for ensuring that adjacent cells differ in only one variable.

Example:

Consider the following Boolean expression:

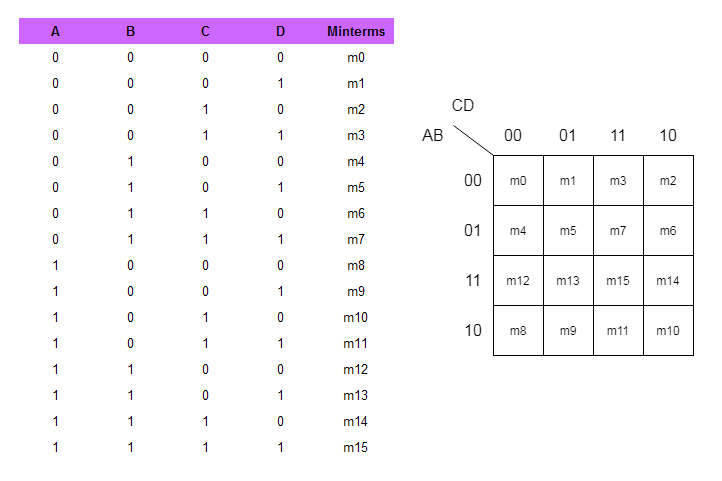
F(A, B, C, D) = Σm(0, 2, 4, 6, 8, 10, 12, 14)

To construct the K-map, we first label the rows with variables C and D, and the columns with variables A and B, using Gray code:

AB	00	01	11	10
00
01
11
10

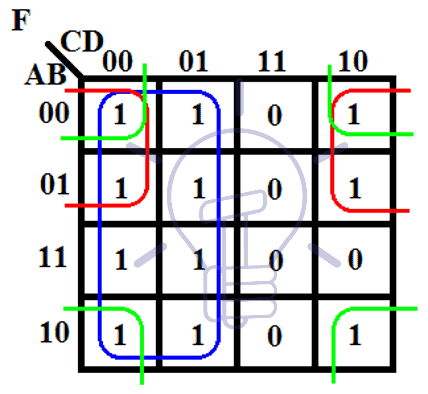
Next, we place a "1" in the cells corresponding to the minterms present in the expression:

AB	00	01	11	10
00	1			1
01		1	1
11
10	1			1

Simplifying Boolean Expressions using K-maps

The power of the K-map lies in its ability to simplify Boolean expressions by identifying and grouping adjacent "1" cells. These groups represent common terms that can be factored out, resulting in a simplified expression.

Rules for Grouping:

• Adjacent Cells: Cells are considered adjacent if they differ in only one variable. This includes cells that share an edge or a corner.
• Groups of 2, 4, 8, …: Groups should contain 2, 4, 8, or any power of 2 cells.
• Largest Possible Groups: Form the largest possible groups, encompassing as many "1" cells as possible.
• Wrap-Around: Cells on opposite edges of the map are considered adjacent.

Example:

In the previous example, we can form the following groups:

• Group 1: Cells (00, 01, 11, 10) in the top row, representing the term A'.
• Group 2: Cells (00, 10) in the leftmost column, representing the term B'.
• Group 3: Cells (01, 11) in the second column, representing the term B.

The simplified expression is then:

F(A, B, C, D) = A' + B' + B

Advantages of using K-maps for Four-Variable Expressions

• Visual Simplification: K-maps provide a visual representation of Boolean expressions, making it easier to identify and group adjacent terms.
• Systematic Approach: The systematic approach of K-maps ensures that all possible simplifications are considered.
• Reduced Complexity: By grouping adjacent cells, K-maps reduce the complexity of Boolean expressions, leading to simpler and more efficient circuits.
• Easy to Understand: The visual nature of K-maps makes them relatively easy to understand and apply, even for beginners.

FAQs on Four-Variable Karnaugh Maps

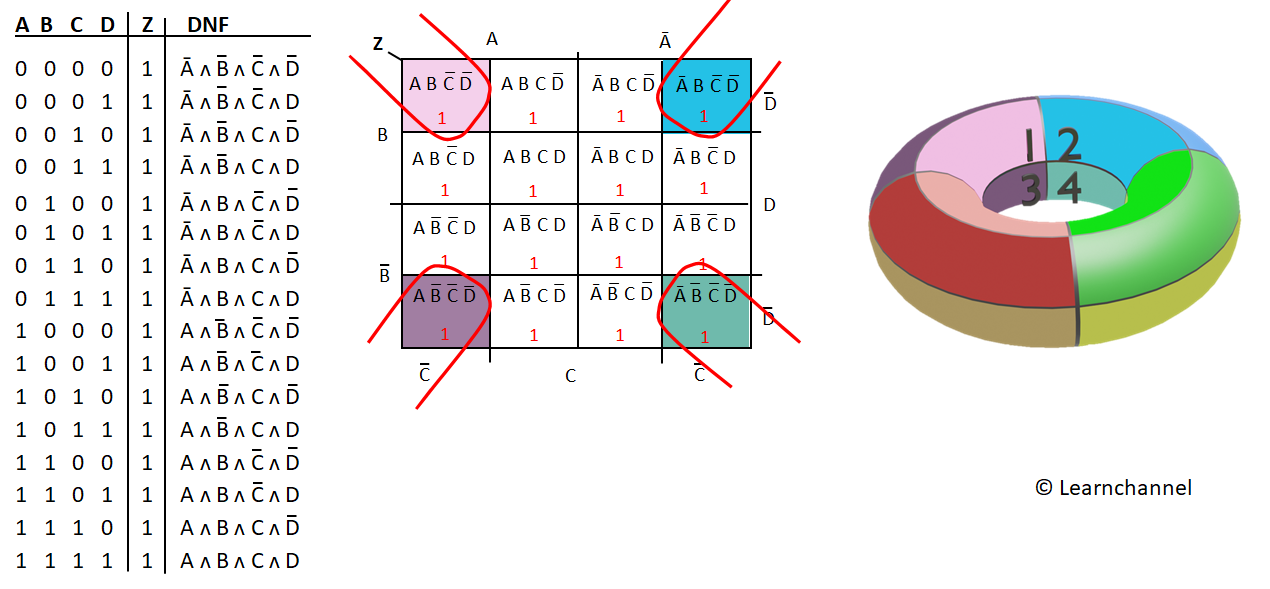
Q: What happens when there are "don’t care" conditions in the expression?

A: "Don’t care" conditions, represented by "X" in the K-map, can be used to simplify the expression further. These conditions can be included in any group, as their value doesn’t affect the output.

Q: How do I handle expressions with a large number of minterms?

A: For expressions with a large number of minterms, it’s recommended to use a combination of K-maps and algebraic simplification techniques.

Q: Can K-maps be used for more than four variables?

A: While K-maps are typically used for up to four variables, it’s possible to use them for five or six variables. However, the visual representation becomes more complex and may require additional techniques.

Tips for Using Four-Variable K-maps Effectively

• Start with a Clear Expression: Ensure that the Boolean expression is clearly defined and written in sum-of-products form.
• Use Gray Code: Label the rows and columns in Gray code to ensure that adjacent cells differ in only one variable.
• Look for Largest Groups: Form the largest possible groups to maximize simplification.
• Don’t Forget Wrap-Around: Consider cells on opposite edges of the map as adjacent.
• Double-Check for Errors: Carefully review the groups and the resulting simplified expression to avoid mistakes.

Conclusion: K-maps as a Powerful Tool for Digital Logic Design

The Karnaugh map remains a valuable tool for simplifying Boolean expressions, particularly for those with four variables. Its visual nature, systematic approach, and ability to reduce complexity make it an essential technique in digital logic design. By mastering the principles of K-maps, engineers and students can efficiently design and implement cost-effective and optimized digital circuits.

Closure

Thus, we hope this article has provided valuable insights into Demystifying the Karnaugh Map: A Comprehensive Guide to Four-Variable Simplification. We appreciate your attention to our article. See you in our next article!