Demystifying the Karnaugh Map: A Powerful Tool for Boolean Expression Simplification

Related Articles: Demystifying the Karnaugh Map: A Powerful Tool for Boolean Expression Simplification

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Demystifying the Karnaugh Map: A Powerful Tool for Boolean Expression Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying the Karnaugh Map: A Powerful Tool for Boolean Expression Simplification

The realm of digital logic circuits is governed by the principles of Boolean algebra, where complex functions are expressed through combinations of logical operations like AND, OR, and NOT. While these functions can be represented in truth tables, they often become unwieldy as the number of variables increases. This is where the Karnaugh map (K-map) emerges as a powerful and intuitive tool for simplifying Boolean expressions, paving the way for more efficient and cost-effective circuit design.

Understanding the K-Map: A Visual Approach to Logic Simplification

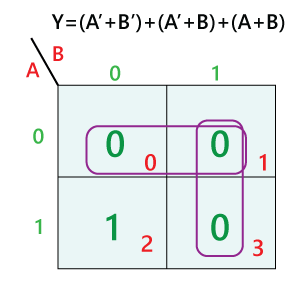
The K-map, named after its inventor Maurice Karnaugh, is a graphical representation of a Boolean function. It provides a visual framework for identifying and grouping adjacent minterms (product terms) that can be simplified through Boolean algebra rules. These rules, such as the consensus theorem and the distributive law, enable us to express the same logical function with fewer terms, thereby reducing the complexity of the corresponding circuit.

Construction and Interpretation of the K-Map

A K-map is constructed based on the number of input variables in the Boolean function. For each variable, there are two possible values (0 and 1), and these values are arranged in a grid-like structure. The rows and columns of the K-map represent different combinations of these values, ensuring that each cell corresponds to a unique minterm.

Key Features of a K-Map:

• Gray Code Ordering: The rows and columns of a K-map are arranged in Gray code order, where only one bit changes between adjacent cells. This ensures that minterms that can be combined for simplification are physically adjacent on the map.
• Grouping of Minterms: The key to simplifying Boolean expressions lies in identifying groups of adjacent 1s on the K-map. These groups represent minterms that can be combined using Boolean algebra rules.
• Group Size and Simplification: The size of the group determines the simplification achieved. A group of two adjacent 1s eliminates one variable, a group of four eliminates two variables, and so on.

Benefits of Using a K-Map Solver

The K-map offers several advantages over traditional algebraic simplification methods:

• Visual Clarity: The graphical representation provides a clear and intuitive way to visualize the relationships between minterms and identify opportunities for simplification.
• Reduced Complexity: By grouping adjacent 1s, the K-map eliminates the need for complex algebraic manipulations, simplifying the process of deriving the minimized Boolean expression.
• Efficiency and Accuracy: The K-map method is highly efficient and less prone to errors compared to manual algebraic simplification, especially for functions with a large number of variables.
• Circuit Optimization: Minimizing the Boolean expression directly translates to a simpler circuit design, leading to reduced component count, lower power consumption, and improved performance.

Applications of K-Map Solvers

K-map solvers are widely used in various fields, including:

• Digital Circuit Design: They are an essential tool for simplifying logic circuits, optimizing their performance, and reducing costs.
• Computer Architecture: K-maps are used in the design of logic units, memory controllers, and other essential components of computer systems.
• Control Systems: They are employed in the development of logic controllers for industrial processes, robotics, and other automation applications.
• Digital Signal Processing: K-maps are used in the design of filters, encoders, decoders, and other signal processing circuits.

FAQs about K-Map Solvers

1. What is the maximum number of variables that can be handled by a K-map?

The maximum number of variables that can be effectively handled by a K-map is four. Beyond that, the complexity of the map becomes too high, and alternative methods like Quine-McCluskey are more suitable.

2. How do I determine the size of a K-map?

The size of a K-map is determined by the number of input variables. A K-map with ‘n’ variables will have 2^n cells. For example, a 3-variable K-map will have 2^3 = 8 cells.

3. What are the different types of K-maps?

There are two main types of K-maps:

• Sum-of-products (SOP) K-map: Used to simplify Boolean expressions in the sum-of-products form.
• Product-of-sums (POS) K-map: Used to simplify Boolean expressions in the product-of-sums form.

4. Can I use a K-map to simplify expressions with don’t care conditions?

Yes, K-maps can be used to simplify expressions with don’t care conditions. These conditions represent input combinations that are not relevant to the output of the function. They can be marked as ‘X’ on the K-map and used to create larger groups for further simplification.

5. Are there any limitations to using K-maps?

While K-maps are powerful tools, they have some limitations:

• Limited to a small number of variables: As mentioned earlier, K-maps are not practical for functions with more than four variables.
• Can be complex for large functions: For functions with a large number of minterms, the K-map can become cumbersome to use.
• Not suitable for all logic functions: K-maps are primarily suited for functions that can be expressed in a sum-of-products or product-of-sums form.

Tips for Using K-Map Solvers Effectively

• Understand the basics: Familiarize yourself with the concepts of Boolean algebra, minterms, and the rules for simplification.
• Choose the appropriate K-map: Select the correct type of K-map (SOP or POS) based on the form of the Boolean expression.
• Start with small examples: Begin by simplifying simple expressions with two or three variables to gain confidence and understanding.
• Use a systematic approach: Follow a structured approach for identifying groups, ensuring that all adjacent 1s are included.
• Verify your results: After obtaining the simplified expression, verify its correctness by comparing it to the original truth table.

Conclusion: The K-Map – A Powerful Tool for Digital Logic Design

The Karnaugh map is an invaluable tool for simplifying Boolean expressions and designing efficient digital circuits. Its visual nature makes it easy to understand and apply, while its effectiveness in reducing complexity and optimizing performance makes it an essential component of any digital logic designer’s toolkit. By mastering the principles and techniques of K-map simplification, engineers can create robust and cost-effective digital systems that meet the demands of modern technology.

Closure

Thus, we hope this article has provided valuable insights into Demystifying the Karnaugh Map: A Powerful Tool for Boolean Expression Simplification. We appreciate your attention to our article. See you in our next article!