Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Simplification

Related Articles: Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Simplification

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Simplification

The world of digital circuits thrives on logic, and within this realm, Karnaugh maps stand as a powerful tool for simplifying Boolean expressions. This method, named after Maurice Karnaugh, provides a visual representation of Boolean functions, allowing for a streamlined process of minimizing complex expressions. This article delves into the essence of Karnaugh maps, exploring their construction, application, and the inherent advantages they offer in simplifying digital logic.

Understanding the Essence of Boolean Expressions

Before embarking on the journey of Karnaugh maps, it’s crucial to grasp the foundation of Boolean algebra. This system, named after George Boole, utilizes variables representing logical states (typically "0" for false and "1" for true) and operators like AND, OR, and NOT to express logical relationships. Boolean expressions, essentially equations within this system, represent the behavior of digital circuits.

Consider a simple example: "A AND B." This expression represents a circuit where the output is "1" (true) only when both inputs A and B are "1." Such expressions, though straightforward in their representation, can become complex when dealing with multiple variables and intricate logical operations.

The Need for Simplification: A Quest for Efficiency

The complexity of Boolean expressions directly translates to the complexity of the corresponding digital circuits. A complex expression translates to a circuit with a multitude of gates, leading to increased cost, size, and power consumption. Simplifying these expressions becomes a critical task in designing efficient and cost-effective digital circuits.

Here, Karnaugh maps step in as a visual aid, enabling a systematic approach to minimizing Boolean expressions. By representing the function in a graphical form, Karnaugh maps facilitate the identification of redundancies and simplifications, ultimately leading to a more efficient circuit implementation.

Constructing the Map: A Visual Representation of Logic

Karnaugh maps are essentially two-dimensional grids where each cell corresponds to a unique combination of input variables. The number of cells is determined by the number of variables: 2^n cells for n variables. The arrangement of cells is crucial, ensuring adjacent cells differ by only one variable.

For instance, a 2-variable Karnaugh map would have 2^2 = 4 cells, representing all possible combinations of two variables (A and B): 00, 01, 11, and 10. These combinations are arranged in a specific order, often referred to as "Gray code," where each cell differs from its neighbor by only one bit.

Mapping the Function: From Expression to Visual

Once the map is constructed, the Boolean expression is "mapped" onto it. Each cell represents a specific combination of inputs, and the value within the cell corresponds to the output of the function for that input combination. This value is typically represented by "1" for true and "0" for false.

For example, consider the expression "A AND B." The corresponding Karnaugh map would have a "1" in the cell representing the input combination "11" (where both A and B are "1"), and "0" in all other cells.

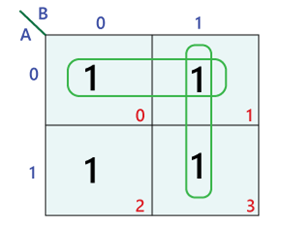
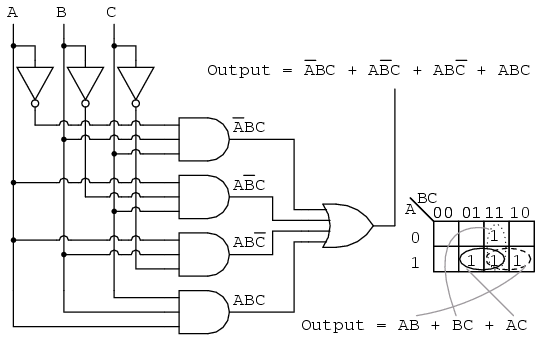
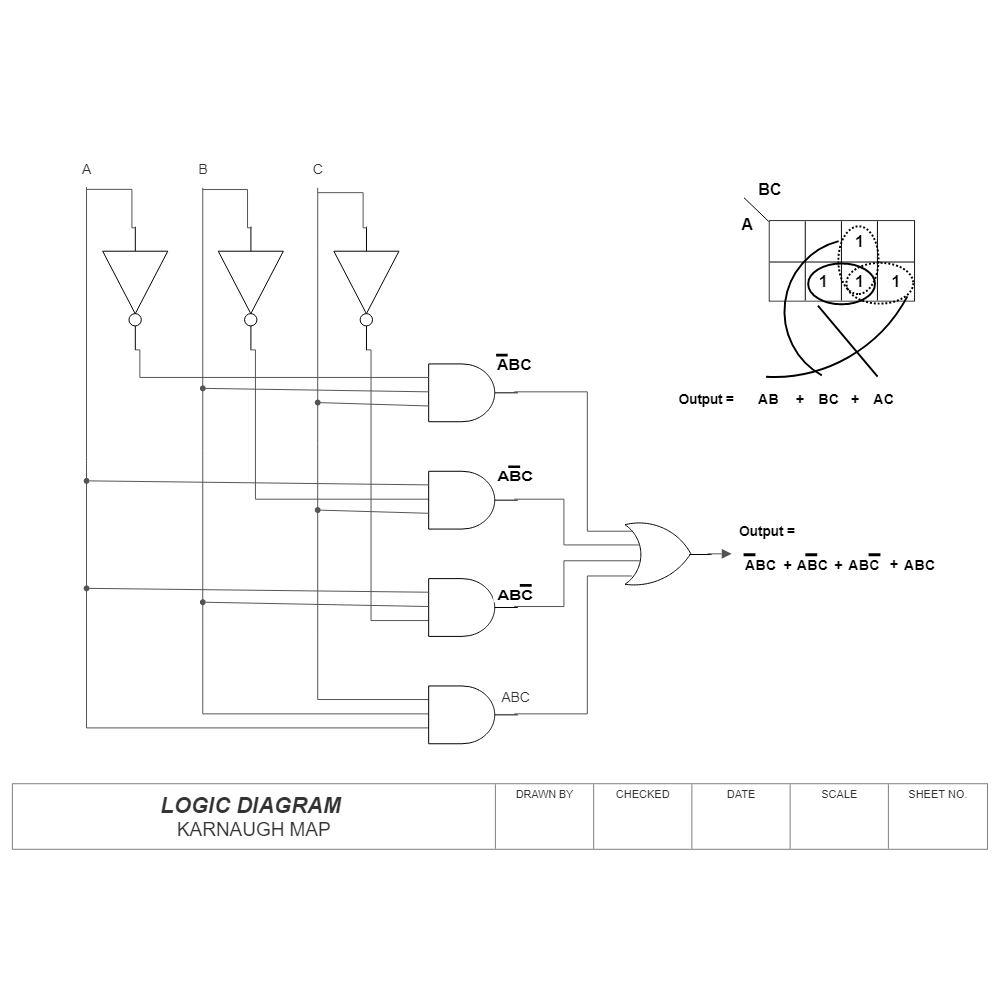
Unveiling Simplifications: The Art of Grouping

The power of Karnaugh maps lies in their ability to visually identify redundancies and simplify the Boolean expression. This is achieved by grouping adjacent cells containing "1"s. The groups must be rectangular, and their size must be a power of two (1, 2, 4, 8, etc.).

Each group represents a simplified term in the final expression. The variables involved in the term are those that remain constant within the group. For instance, a group covering the cells "01" and "11" represents the term "B," as the variable B remains "1" in both cells while A changes.

Applying the Technique: A Step-by-Step Guide

Let’s illustrate the process with a more complex example:

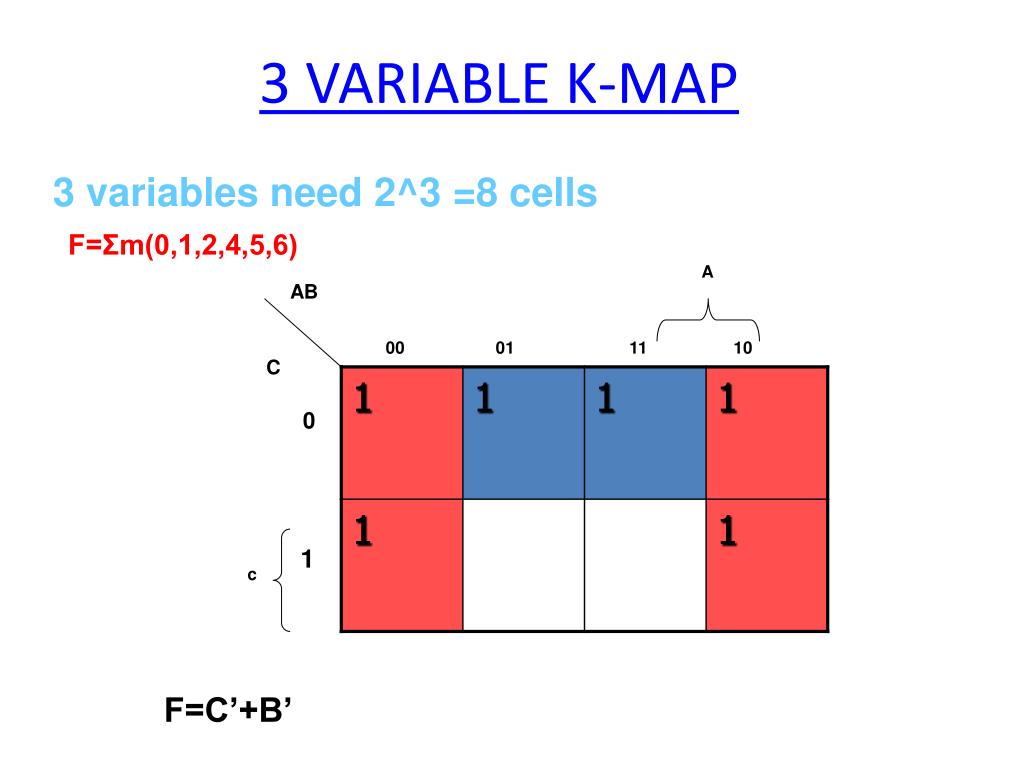
Expression: F(A, B, C) = Σ(0, 1, 2, 3, 6)

This expression represents a function with three variables (A, B, C) and outputs "1" for input combinations 0, 1, 2, 3, and 6.

Step 1: Constructing the Karnaugh Map

We need a 3-variable map (2^3 = 8 cells). The cells are arranged in Gray code order:

     |  00  |  01  |  11  |  10  |
     |------|------|------|------|
  0  |      |      |      |      |
     |------|------|------|------|
  1  |      |      |      |      |
     |------|------|------|------|

Step 2: Mapping the Function

The input combinations corresponding to the minterms (0, 1, 2, 3, 6) are marked with "1"s in the map:

     |  00  |  01  |  11  |  10  |
     |------|------|------|------|
  0  |  1  |  1  |  1  |  1  |
     |------|------|------|------|
  1  |  0  |  1  |  0  |  0  |
     |------|------|------|------|

Step 3: Grouping the "1"s

We identify the largest possible groups of adjacent "1"s:

• A group of four "1"s covering cells (00, 01, 11, 10) in the top row.
• A single "1" in cell (01) in the bottom row.

Step 4: Deriving the Simplified Expression

• The group of four represents the term "1" (as all variables change within the group).
• The single "1" represents the term "A’BC" (as A is "0," B is "1," and C is "1" in this cell).

Simplified Expression: F(A, B, C) = 1 + A’BC

This expression is significantly simpler than the original, representing the same logical function but with fewer terms and gates.

Benefits of Karnaugh Maps: A Powerful Tool for Simplification

The use of Karnaugh maps offers numerous advantages in simplifying Boolean expressions and designing efficient digital circuits:

• Visual Approach: The graphical representation provides a clear and intuitive understanding of the Boolean function, aiding in identifying patterns and redundancies.
• Systematic Simplification: The process of grouping "1"s offers a structured and systematic approach to minimizing the expression, ensuring minimal redundancy.
• Reduced Complexity: Simplified expressions translate to circuits with fewer gates, resulting in lower cost, size, and power consumption.
• Improved Performance: Reduced complexity leads to faster processing times and improved overall circuit performance.
• Easy Implementation: The simplified expressions are easily translated into digital circuits using readily available logic gates.

Beyond Basics: Exploring Advanced Applications

While Karnaugh maps are particularly effective for functions with up to four variables, their application can be extended to handle more complex scenarios:

• Don’t Cares: In certain cases, specific input combinations might not be relevant to the circuit’s operation. These "don’t cares" can be marked on the map and used to further simplify the expression by including them in groups.
• Multi-Level Logic: Karnaugh maps can be employed for simplifying multi-level logic circuits, where outputs of one circuit act as inputs to another. This involves applying the mapping technique to each level of logic.
• Product of Sums (POS) Simplification: While typically used for minimizing Sum of Products (SOP) expressions, Karnaugh maps can also be adapted for simplifying Product of Sums expressions by grouping "0"s instead of "1"s.

FAQs about Karnaugh Maps: Addressing Common Queries

Q: What are the limitations of Karnaugh maps?

A: Karnaugh maps become less practical for functions with more than four variables due to the increasing complexity of the map. For higher-order functions, other methods like Quine-McCluskey algorithm or computer-aided design tools are preferred.

Q: Can Karnaugh maps handle functions with multiple outputs?

A: Yes, Karnaugh maps can be used for functions with multiple outputs by creating a separate map for each output. The simplification process is then applied individually to each map.

Q: How do I handle "don’t cares" in Karnaugh maps?

A: "Don’t cares" are marked with an "X" on the map. They can be included in groups to further simplify the expression, as their output value doesn’t affect the circuit’s functionality.

Q: What are the common errors to avoid when using Karnaugh maps?

A: Common errors include incorrect grouping of cells (non-rectangular or not powers of two), overlooking adjacent cells in different rows or columns, and misinterpreting the simplified terms from the groups.

Tips for Effective Karnaugh Map Utilization: Mastering the Technique

• Start with a Clear Understanding: Ensure a firm grasp of Boolean algebra and logic operations before attempting Karnaugh map simplification.
• Practice Makes Perfect: Utilize numerous examples and exercises to gain proficiency in constructing, mapping, and grouping cells on the map.
• Pay Attention to Details: Be meticulous in identifying adjacent cells, ensuring they differ by only one variable, and accurately deriving the simplified terms from each group.
• Don’t Overlook "Don’t Cares": Utilize "don’t cares" strategically to achieve further simplification.
• Combine with Other Methods: For higher-order functions, consider using Karnaugh maps in conjunction with other simplification techniques or computer-aided design tools.

Conclusion: Embracing the Power of Visual Simplification

Karnaugh maps stand as a powerful tool for simplifying Boolean expressions, offering a visual approach to identifying redundancies and minimizing complexity. By understanding their construction, mapping process, and grouping techniques, designers can leverage their benefits to create efficient and cost-effective digital circuits. As technology continues to evolve, the ability to simplify complex logic remains a crucial skill for engineers and developers, making Karnaugh maps an indispensable resource in the world of digital design.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Simplification. We appreciate your attention to our article. See you in our next article!