Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions

Related Articles: Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions

In the realm of digital logic design, the ability to efficiently simplify complex Boolean expressions is paramount. This simplification not only enhances circuit readability and understanding but also contributes to the creation of more economical and robust circuits. One powerful tool that aids in this endeavor is the Karnaugh map, a graphical method for simplifying Boolean expressions that has become an indispensable tool for engineers and designers.

Understanding the Fundamentals of Karnaugh Maps

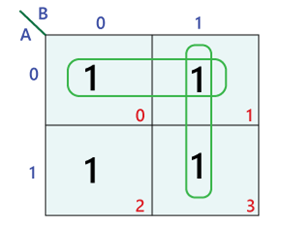
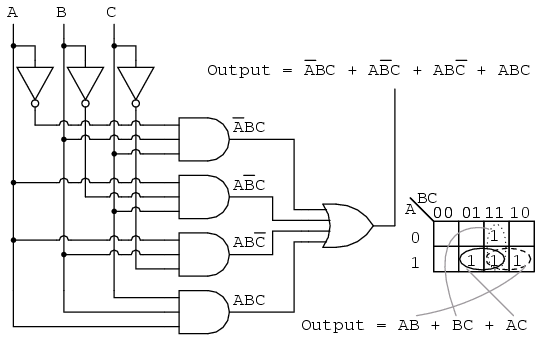
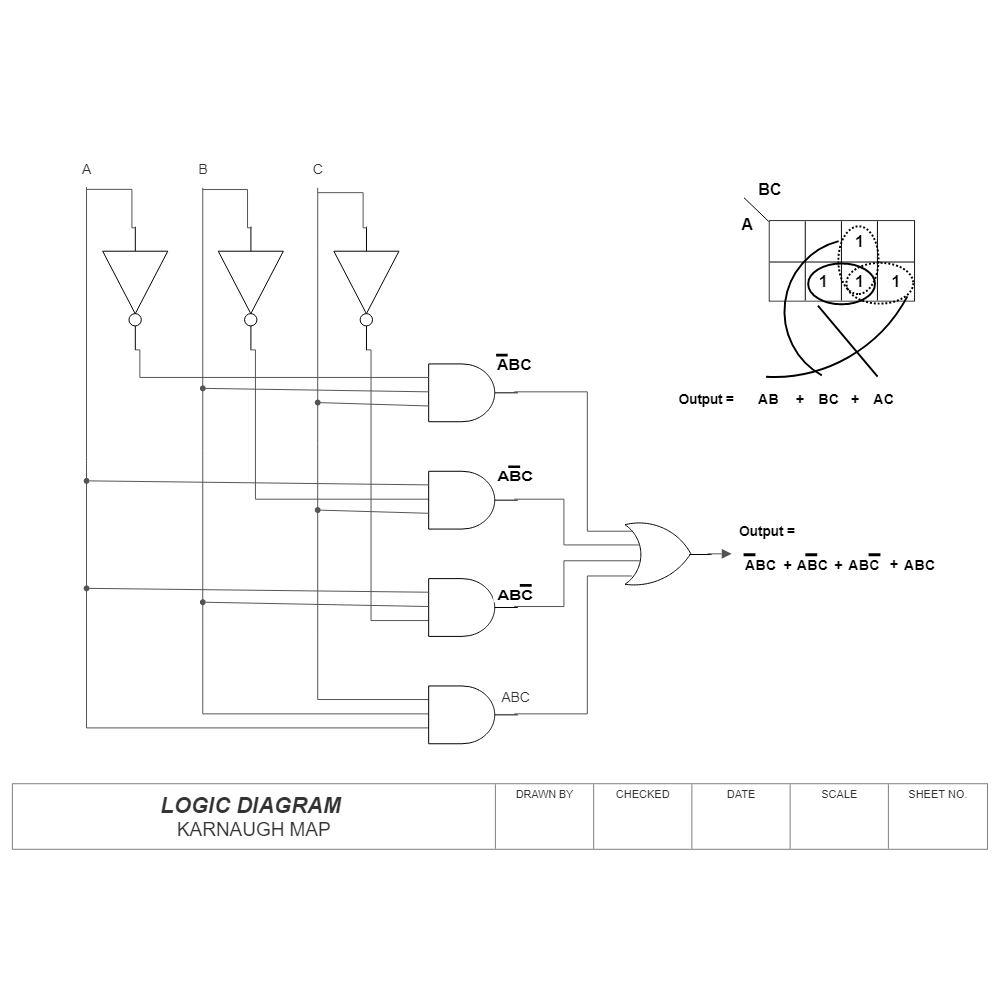
A Karnaugh map, often referred to as a K-map, is a visual representation of a truth table, a tabular depiction of all possible combinations of input variables and their corresponding output values. The map’s structure is designed to facilitate the identification of adjacent minterms (product terms) that can be combined, leading to the simplification of the Boolean expression.

The Essence of Karnaugh Map Construction:

1. Determining the Number of Variables: The number of variables in the Boolean expression dictates the size of the Karnaugh map. For instance, a two-variable expression requires a 2×2 map, a three-variable expression needs a 2×4 map, and so on.

2. Defining the Map’s Structure: Each cell in the Karnaugh map represents a unique combination of input variables. The arrangement of cells ensures that adjacent cells differ in only one variable. This adjacency is crucial for identifying minterms that can be combined.

3. Populating the Map: Each cell is assigned a ‘1’ or ‘0’ based on the corresponding output value in the truth table. Cells with a ‘1’ represent minterms that contribute to the simplified expression.

Simplifying Boolean Expressions with Karnaugh Maps

The primary advantage of using Karnaugh maps lies in their ability to streamline the simplification process. The map’s visual representation allows for the quick identification of adjacent minterms that can be combined, leading to a more concise expression.

Key Principles of Karnaugh Map Simplification:

1. Grouping Adjacent Cells: Adjacent cells containing ‘1’s are grouped together. These groups can be horizontal, vertical, or diagonal, as long as they are contiguous.

2. Maximizing Group Size: The goal is to form the largest possible groups of adjacent cells containing ‘1’s. Larger groups correspond to simpler terms in the simplified expression.

3. Power of Two: The number of cells in each group should be a power of two (1, 2, 4, 8, etc.).

4. Covering All ‘1’s: All cells containing ‘1’s must be included in at least one group.

5. Minimizing the Number of Groups: The fewer groups required to cover all ‘1’s, the simpler the final expression.

6. Don’t Care Conditions: In some cases, certain input combinations may not be relevant to the circuit’s functionality. These "don’t care" conditions can be represented with an ‘X’ on the Karnaugh map. They can be used strategically to further simplify the expression by including them in groups.

Practical Applications of Karnaugh Maps

Karnaugh maps have proven invaluable in various fields, particularly in digital logic design and circuit optimization. Here are some key applications:

• Digital Circuit Design: Karnaugh maps are instrumental in simplifying Boolean expressions that represent the behavior of digital circuits. This simplification leads to circuits with fewer gates, reducing cost, power consumption, and complexity.

• Logic Function Minimization: Karnaugh maps enable the minimization of logic functions, resulting in more efficient and compact circuits.

• Digital Circuit Analysis: They can be used to analyze existing circuits, identifying potential areas for simplification and optimization.

• Fault Detection and Diagnosis: Karnaugh maps can aid in fault detection and diagnosis by visually highlighting potential issues in the circuit’s logic.

• Educational Tool: Karnaugh maps are widely used in educational settings to teach students about Boolean algebra and digital logic design.

Illustrative Example: Simplifying a Boolean Expression

Let’s consider a simple example to demonstrate the power of Karnaugh maps. Suppose we have the following Boolean expression:

F(A, B, C) = Σ(0, 1, 2, 3, 5)

This expression represents a function with three input variables (A, B, C) and five minterms (0, 1, 2, 3, 5). To simplify this expression, we follow these steps:

1. Construct the Karnaugh Map: Create a 2×4 Karnaugh map for three variables. Each cell corresponds to a unique combination of input values.

2. Populate the Map: Assign ‘1’ to the cells corresponding to the minterms (0, 1, 2, 3, 5) and ‘0’ to the remaining cells.

3. Group Adjacent Cells: Identify the largest possible groups of adjacent cells containing ‘1’s. In this case, we can form two groups:

   • Group 1: Covers cells (0, 1, 2, 3)
   • Group 2: Covers cells (1, 5)

4. Derive the Simplified Expression: For each group, identify the input variables that remain constant within the group.

   • Group 1: A = 0, B = 0 (regardless of C)
   • Group 2: B = 1, C = 1 (regardless of A)

   Therefore, the simplified expression is:

   F(A, B, C) = A'B' + BC

This simplified expression is equivalent to the original expression but requires fewer gates to implement, making the circuit more efficient and cost-effective.

FAQs about Karnaugh Maps

1. What are the limitations of Karnaugh maps?

While Karnaugh maps are powerful tools, they become less efficient as the number of input variables increases. For expressions with more than five variables, the map’s size and complexity become unwieldy, making manual simplification challenging.

2. Are there alternative methods for Boolean expression simplification?

Yes, there are other techniques like the Quine-McCluskey method, which is more systematic and can handle expressions with a larger number of variables. However, Karnaugh maps remain a valuable tool for smaller expressions and offer a more intuitive visual approach.

3. How do Karnaugh maps handle "don’t care" conditions?

"Don’t care" conditions, represented by ‘X’ on the map, can be included in groups to further simplify the expression. They provide flexibility in combining cells, potentially leading to more concise solutions.

4. Can Karnaugh maps be used for functions with multiple outputs?

Yes, Karnaugh maps can be used for functions with multiple outputs. In such cases, a separate map is created for each output, and the simplification process is applied independently for each map.

5. Are there any online tools for creating and simplifying Karnaugh maps?

Yes, several online tools are available that provide interactive Karnaugh map generators and simplifiers. These tools can be helpful for visualization, experimentation, and verification.

Tips for Effective Use of Karnaugh Maps

• Start with a Clear Truth Table: Ensure the truth table is accurate and complete before creating the Karnaugh map.

• Choose the Right Map Size: Select the appropriate map size based on the number of input variables.

• Group Strategically: Focus on forming the largest possible groups while covering all ‘1’s.

• Consider Don’t Cares: Utilize "don’t care" conditions to your advantage for potential simplification.

• Verify Your Results: After simplification, double-check your results by comparing the simplified expression with the original truth table.

Conclusion

Karnaugh maps are a valuable tool for simplifying Boolean expressions, leading to more efficient, compact, and cost-effective digital circuits. They provide a visual and intuitive approach to logic minimization, making them widely used in digital design, analysis, and education. While limitations exist for complex expressions, their effectiveness for smaller functions and their intuitive nature make them a powerful tool for engineers and designers alike.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Simplifying Boolean Expressions. We thank you for taking the time to read this article. See you in our next article!