Unlocking the Power of Logic: A Comprehensive Guide to Karnaugh Maps and Their Applications
Related Articles: Unlocking the Power of Logic: A Comprehensive Guide to Karnaugh Maps and Their Applications
Introduction
With enthusiasm, let’s navigate through the intriguing topic related to Unlocking the Power of Logic: A Comprehensive Guide to Karnaugh Maps and Their Applications. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
- 1 Related Articles: Unlocking the Power of Logic: A Comprehensive Guide to Karnaugh Maps and Their Applications
- 2 Introduction
- 3 Unlocking the Power of Logic: A Comprehensive Guide to Karnaugh Maps and Their Applications
- 3.1 Understanding the Fundamentals of Karnaugh Maps
- 3.2 Constructing Karnaugh Maps: A Step-by-Step Approach
- 3.3 Simplifying Boolean Expressions with Karnaugh Maps
- 3.4 Illustrative Examples of K-Map Applications
- 3.5 Benefits of Utilizing Karnaugh Maps in Logic Design
- 3.6 FAQs Regarding Karnaugh Maps and Their Applications
- 3.7 Tips for Effective Utilization of Karnaugh Maps
- 3.8 Conclusion
- 4 Closure
Unlocking the Power of Logic: A Comprehensive Guide to Karnaugh Maps and Their Applications
Karnaugh maps, often referred to as K-maps, are a visual and intuitive tool used in digital logic design to simplify Boolean expressions and derive optimized logic circuits. This technique offers a graphical representation of truth tables, enabling the identification of patterns and the simplification of complex logical functions. By utilizing K-maps, designers can achieve significant reductions in the number of logic gates required, leading to more efficient, compact, and cost-effective circuits.
Understanding the Fundamentals of Karnaugh Maps
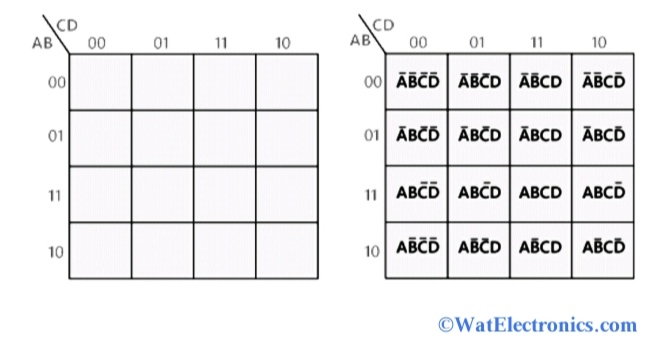
At the heart of K-maps lies the concept of representing Boolean expressions in a visually organized manner. This representation is achieved through a grid structure, where each cell corresponds to a unique combination of input variables. The arrangement of cells within the map is crucial, as it ensures that adjacent cells differ by only one variable, facilitating the identification of logical relationships.
Key Components of a Karnaugh Map:
- Input Variables: The number of input variables determines the size of the map. For example, a two-variable K-map requires a 2×2 grid, a three-variable map requires a 2×4 grid, and so on.
- Cells: Each cell in the map represents a unique combination of input variable values.
- Minterms: Each cell is assigned a minterm, which is a product term representing the specific combination of input values corresponding to that cell.
- Adjacency: Cells that are adjacent to each other (horizontally or vertically, but not diagonally) differ in only one input variable. This adjacency is crucial for identifying groups of minterms that can be combined to simplify the Boolean expression.
Constructing Karnaugh Maps: A Step-by-Step Approach
The process of constructing a K-map involves translating the truth table of a Boolean function into a graphical representation. This involves assigning each minterm of the truth table to its corresponding cell on the map.
Steps to Construct a Karnaugh Map:
- Determine the Number of Variables: Identify the number of input variables in the Boolean function.
- Create the Grid: Construct a grid with the appropriate number of rows and columns based on the number of input variables. The number of rows and columns is determined by the power of two that is closest to the number of input variables. For example, a 3-variable K-map will have 2 rows and 4 columns (2^2 x 2^1 = 2^3).
- Label the Rows and Columns: Label the rows and columns with the input variables and their corresponding values. The order of the variables and their values is crucial to ensure that adjacent cells differ by only one variable.
- Assign Minterms: Assign each minterm from the truth table to its corresponding cell on the K-map. The minterm is represented by a "1" if the output of the function is "1" for that particular input combination, and a "0" if the output is "0".
Simplifying Boolean Expressions with Karnaugh Maps
The true power of K-maps lies in their ability to simplify Boolean expressions by identifying groups of adjacent minterms that can be combined. These groups, known as "loops," represent common terms in the Boolean expression that can be factored out, leading to a more simplified form.
Rules for Loop Formation:
- Adjacent Cells: Loops can only be formed by grouping adjacent cells, either horizontally or vertically, but not diagonally.
- Power of Two: The number of cells in a loop must be a power of two (1, 2, 4, 8, etc.).
- Maximum Coverage: Aim to cover all the "1" cells in the map with the fewest possible loops.
- Don’t Care Conditions: Cells marked with "X" represent "don’t care" conditions, where the output of the function is irrelevant. These cells can be included in loops to further simplify the expression.
Procedure for Simplifying Boolean Expressions:
- Identify Loops: Encircle groups of "1" cells on the K-map, following the rules of loop formation.
- Write the Product Terms: For each loop, write down the product term representing the input variables common to all cells within the loop.
- Combine Product Terms: Combine the product terms obtained from all loops using the OR operator.
Illustrative Examples of K-Map Applications
Example 1: Simplifying a 3-Variable Boolean Function:
Consider the following truth table for a 3-variable Boolean function:
| A | B | C | Output |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
The corresponding K-map is shown below:
C' C
A B' B
0 0 1
0 0 1
1 1 1
1 0 1From the map, we can identify two loops:
- Loop 1: Covers the cells (0, 0, 1), (0, 1, 1), (1, 1, 1), and (1, 0, 1). The common variables are C and A’, resulting in the product term C*A’.
- Loop 2: Covers the cell (0, 1, 1). The common variable is B, resulting in the product term B.
Combining these product terms using OR, we obtain the simplified Boolean expression:
*Output = CA’ + B**
Example 2: Using Don’t Care Conditions:
Suppose we have a 4-variable Boolean function with the following truth table:
| A | B | C | D | Output |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | X |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | X |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | X |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | X |
The corresponding K-map is:
CD' CD C'D C'D'
A B' B
0 1 X 1 1
0 1 X 1 1
1 1 X 1 1
1 1 X 1 1We can form a single loop covering all the "1" cells and the "X" cells, resulting in the simplified expression:
Output = 1
The "don’t care" conditions allowed us to cover all the "1" cells with a single loop, leading to a significantly simpler expression.
Benefits of Utilizing Karnaugh Maps in Logic Design
The use of K-maps in digital logic design offers several significant advantages:
- Simplified Logic Circuits: K-maps facilitate the derivation of minimal Boolean expressions, leading to circuits with fewer logic gates. This results in smaller, more efficient, and less costly circuits.
- Improved Readability: K-maps provide a clear and visually intuitive representation of Boolean functions, making it easier to understand and analyze logic circuits.
- Reduced Design Time: The graphical nature of K-maps allows for quicker and more efficient design processes, especially for complex logic functions.
- Error Detection: The use of K-maps can help identify potential errors in the design process by ensuring that all possible input combinations are accounted for.
FAQs Regarding Karnaugh Maps and Their Applications
Q1: How do I determine the size of a K-map for a given number of variables?
A: The size of a K-map is determined by the power of two that is closest to the number of input variables. For example, a 3-variable K-map will have 2 rows and 4 columns (2^2 x 2^1 = 2^3).
Q2: Can I use a K-map for functions with more than four variables?
A: While K-maps are most effective for functions with up to four variables, they can be used for functions with more variables by employing a combination of multiple maps. However, the complexity of the process increases significantly with a higher number of variables.
Q3: What are the limitations of using Karnaugh maps?
A: K-maps become increasingly complex and cumbersome to use for functions with more than four variables. Additionally, the process of identifying optimal loops can be challenging, especially for large maps.
Q4: Are there alternative methods for simplifying Boolean expressions?
A: Yes, there are other methods for simplifying Boolean expressions, such as the Quine-McCluskey method and Boolean algebra manipulation. These methods are more algorithmic and can be applied to functions with any number of variables.
Q5: What are some real-world applications of Karnaugh maps?
A: K-maps find applications in various fields, including:
- Digital Circuit Design: Simplifying logic circuits for digital systems, such as computers, mobile devices, and embedded systems.
- Computer Architecture: Designing efficient control units and data paths for microprocessors.
- Digital Signal Processing: Implementing digital filters and other signal processing algorithms.
- Robotics and Automation: Controlling actuators and sensors in robotic systems.
Tips for Effective Utilization of Karnaugh Maps
- Start with a Clear Truth Table: Ensure that the truth table for the Boolean function is accurate and complete.
- Label Rows and Columns Carefully: The order of variables and their values is crucial for correct adjacency.
- Use a Systematic Approach: Follow a structured approach to identify loops, ensuring that all "1" cells are covered.
- Utilize Don’t Care Conditions: Include "don’t care" conditions in loops to further simplify the expression.
- Verify the Simplified Expression: After obtaining the simplified expression, verify its correctness by comparing it to the original truth table.
Conclusion
Karnaugh maps are a powerful and intuitive tool for simplifying Boolean expressions and optimizing logic circuits. By providing a visual representation of truth tables, K-maps enable designers to identify patterns and derive efficient logical functions. While alternative methods exist, K-maps remain a valuable technique for simplifying logic circuits, particularly for functions with up to four variables. Their ability to streamline design processes, reduce circuit complexity, and improve readability makes them a fundamental tool in the field of digital logic design.
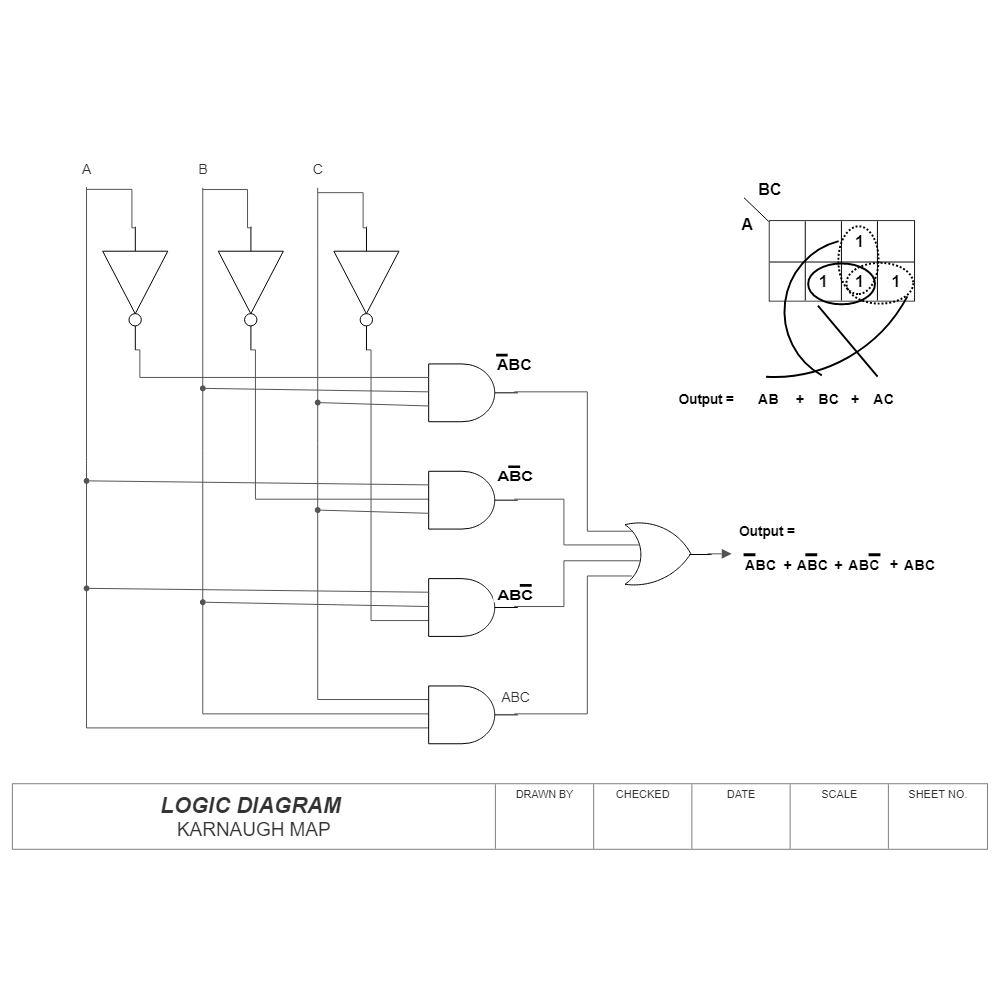

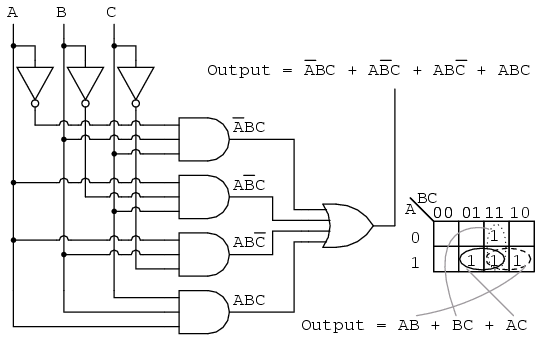
![[DIAGRAM] Logic Diagram Karnaugh Map - WIRINGSCHEMA.COM](https://i.ytimg.com/vi/eGNdpwOrsTo/maxresdefault.jpg)
![[DIAGRAM] Logic Diagram Karnaugh Map - MYDIAGRAM.ONLINE](http://web.cecs.pdx.edu/~mcnames/ECE171/Lectures/Lecture10/Karnaugh6Var1a.gif)
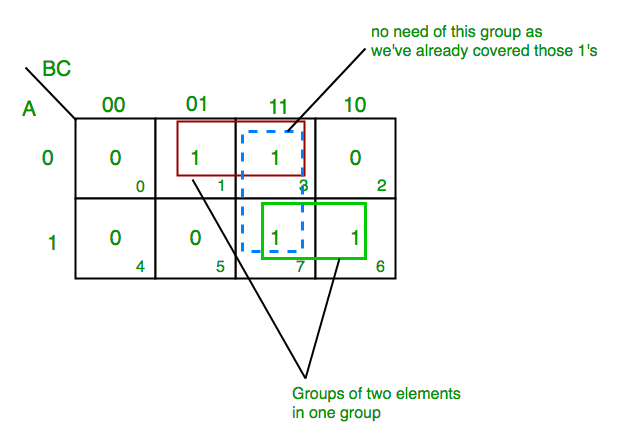
Closure
Thus, we hope this article has provided valuable insights into Unlocking the Power of Logic: A Comprehensive Guide to Karnaugh Maps and Their Applications. We appreciate your attention to our article. See you in our next article!












































/beckyg-63446fd15a7d47289a962ab987a9d920.png)





:max_bytes(150000):strip_icc()/bekcy-845181356dd64944b0c4c4e3476d2097.png)



























